Project information

• Category: Linear & Discreet Optimization
• Done for: University Module
• Project date: 2023
• Project URL: https://github.com/Daniel2tio/Car-Rental-Optimization

This project involves solving a complex optimization problem using both LPSolve and Excel towards a car rental company.

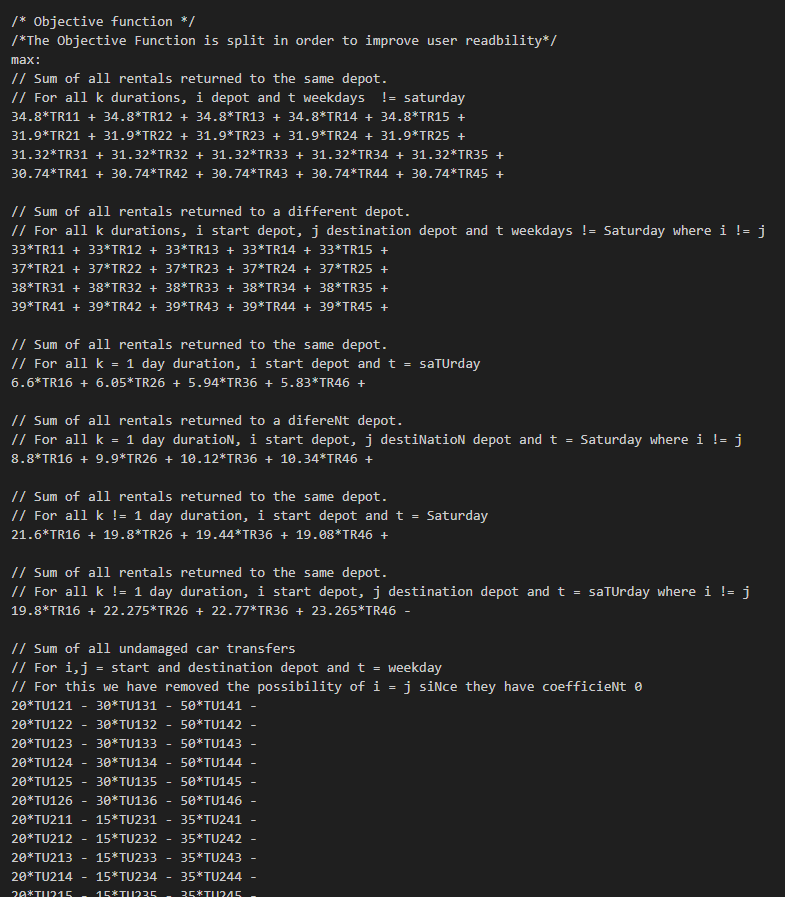
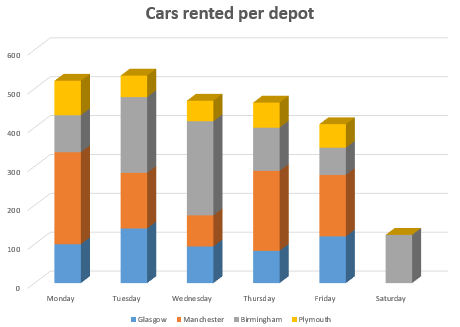
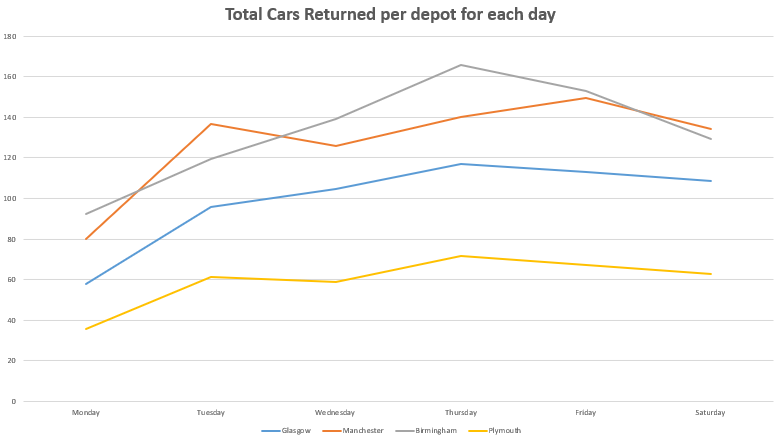
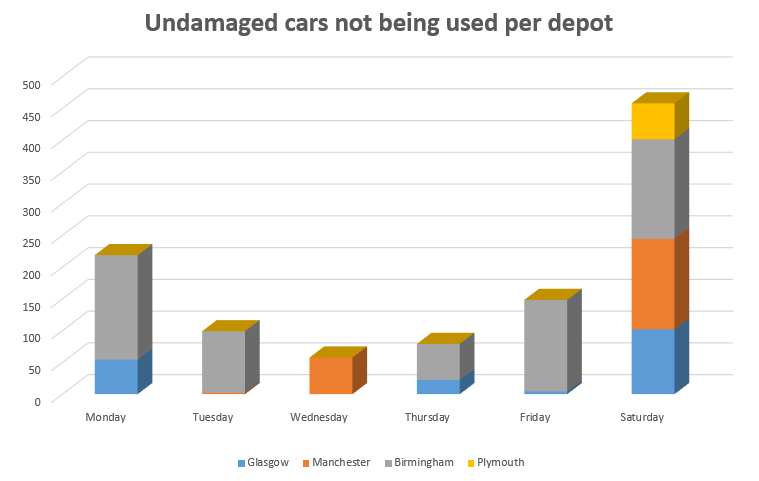
The car rental optimization problem involves maximizing the revenue and minimizing the costs associated with renting and transferring cars between depots. Decision variables include the total number of cars, the number of undamaged and damaged cars at each depot per day, the number of cars rented out, and those transferred between depots. The objective function seeks to maximize revenue from rentals returned to the same or different depots, accounting for different durations and days of the week, while considering transfer and opportunity costs. Additionally, the cost of expanding the fleet is factored in. Constraints ensure the balance of cars (undamaged and damaged) in each depot daily. They track cars entering and leaving depots through rentals, repairs, and transfers. The constraints also include coefficients representing the fraction of cars returned in various conditions (undamaged or damaged) and the impact of transfers and repairs on the available fleet. The goal is to ensure that the total number of cars at each depot at the end of each day meets specific requirements, maintaining the operational balance across the network.